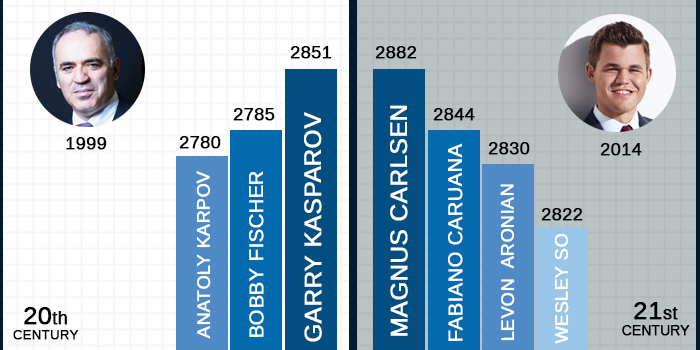
According to FIDE rankings, Magnus Carlsen is the strongest player in the world. His highest rating was 2882 which is the highest ever.  Garry Kasparov reached 2851 points in FIDE list in July of 1999. And Bobby Fischer’s highest rating was only 2785 on April 1972.

But the question is: Can we compare their abilities according to their rating?  The average Elo rating of top players has risen over time. Thus it is still question can we claim that Carlsen is a stronger chess player than Fischer was, judging by their ratings? And how objective would that judgment be?

Here you can see world’s top 4 highest ratings ever.

Rank	Rating	Player	Year-month
1	2882	Magnus Carlsen	May 2014
2	2851	Garry Kasparov	July 1999
3	2844	Fabiano Caruana	October 2014
4	2830	Levon Aronian	March 2014

 

ELO rating system is being used by FIDE, USCF and online chess servers. The chess rating system is a method of estimating the strength of a chess player. Even though the theory of the current system was developed as far back as the late 1950s, the International chess federation only adopted the rating system in 1970. 

 

ELO method is based on a precise mathematical equation. Elo Rating Algorithm is widely used to rank players in many competitive games.  In some cases, the rating system can discourage game activity for players who wish to protect their rating. If one player is some points higher rated than his opponent he is expected to win.

Even though according to ELO system a higher rated player is more likely to win,  it does not automatically mean he will win the game. Relating increases or decreases in one’s ratings over time to change in ability is very tricky business, it’s overall credibility needs to be seen in the context of at least the major issue described above.

Time factors (inflation/deflation)

When a player talks about “1900 rating strength” he or she is doing so with the implicit understanding that a rating of 1900 connotes a specific level of ability. Moreover, a general belief exists that “1900 strength” this year should be “1900 strength” next year,  6 years from now and in 20 years from now and if somehow this does not happen, then something is wrong with the rating system.

The fact is that a rating system solely based on game outcome of players whose abilities may be changing over time is unable to guarantee that a particular rating will connote the same ability over time  This is an observation pointed out by written and computer consultant John Bensley who asserts that ratings can be used to relative abilities, not absolute abilities. 

As Elo argued, the average ELO among rated players has a great tendency to decrease over time. If no new players enter or leave the pool of rated players than every gain in rating by one player would result in a decrease in rating by another player by an equal amount. Thus rating points would be conserved and the average rating of all players would remain constant over time.

But typically players who enter the rating pool are assigned low provisional ratings and players who leave the rating pool are experienced players who have above-average ratings, The net effect of this flux of players lowers the overall average rating.

Remaining players, in all likelihood,  will compete against underrated opponents who are improving and will on average obtain lower ratings at the expense of the underrated players. However, practice shows that the average Elo rating of top players has risen over time.

We can identify several possible goals for maintaining characteristics of the overall rating pool. One possible goal is to force the median rating or some percentile of all active players to the prespecified rating by periodically adding a fixed amount to all ratings.

Even though adjustments in the rating system have been implemented to counteract rating drift, being concerned about changes in an average rating of the tournament chess playing population inherently depends on the goals of the rating system.

The rating system by itself only makes assumptions about differences in players’ ratings, not in the actual value. So, if 500 were subtracted or added to everyone’s rating to stop rating deflation, the rating system would still be just as valid, because differences in player’s ratings would still remain the same. 

One possible direction of effort is to develop techniques to make ratings connote the same ability over time through external means, though the merit of any of these approaches is certainly arguable. A computer chess program can be viewed as having a fixed ability.

The ratings of several chess programs can be accurately estimated, then this ratings can be used as fixed “anchors” in the rating system. A compelling argument against this approach is that humans play differently against chess programs than they do against other humans. Also, implementing such a procedure regularly may be impractical and expensive.

Rank	Name	Title	Country	Rating	B-Year
1	Magnus Carlsen	GM	NOR	2843	1990
2	Fabiano Caruana	GM	USA	2816	1992
3	Shakhriyar Mamedyarov	GM	AZE	2808	1985
4	Ding Liren	GM	CHN	2798	1992
5	Vladimir Kramnik	GM	RUS	2792	1975
6	Maxime Vachier-Lagrave	GM	FRA	2789	1990
7	Anish Giri	GM	NED	2782	1994
8	Sergey Karjakin	GM	RUS	2782	1990
9	Wesley So	GM	USA	2778	1993
10	Hikaru Nakamura	GM	USA	2769	1987

Top 100 Players June 2018

A somewhat more scientific approach for ratings connoting the same ability over time involves designing a chess test to measure a chess ability and then fitting a statistical model to predict chess ratings with reasonable accuracy from the chess test. A series of chess questions could be constructed to taste ability in all phases of the game.

This approach, while making use of an external source to measure chess ability other than game results, has benefits of identifying the aspects that separate weak chess players from strong ones. On the downside, assessing the accuracy of the test is now a new source of variability, and could increase the difficulty in measuring playing strength. 

Recognising that the rating system may not be able to provide an absolute of chess ability but a rather only measure relative to other rated players means that even though one’s rating may be changing, it is not clear whether it is changing relative to the entire pool or rated players.

The argument of “rating deflation” involves examining the flux of chess players into and out of the player population. Therefore, Elo ratings still provide a useful mechanism for providing a rating based on the opponent's rating. If you play enough games, you will get to your 'True Rating' eventually. This is true.

• ← Предыдущий
• Следующий →